Шнурки Гаусса
Приветствуем вас на сайте команды "Шнурки Гаусса"!
Что такое <<цепная дробь>>?
Понятие цепной дроби
Цепная дробь (или непрерывная дробь) - это выражение вида
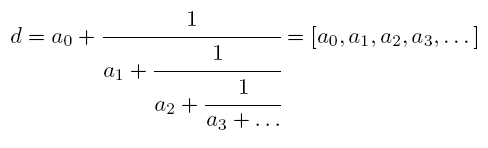
Числа a0, a1, a2, a3,… называются элементами цепной дроби. В такую дробь может быть разложено любое вещественное число. Цепная дробь бывает конечной или бесконечной, причём в виде конечной цепной дроби может быть представлено только рациональное число.
У бесконечных цепных дробей возможно наличие периода (бесконечно повторяющегося элементов цепной дроби), такие цепные дроби называются периодическими. В виде периодической цепной дроби может быть представлена только квадратичная иррациональность (то есть такое иррациональное число, которое может являться корнем квадратного уравнения с целыми коэффициентами). Например, золотое сечение (иррациональная математическая константа, являющаяся корнем квадратного уравнения x2-x-1 = 0) представляется в виде цепной дроби [1,1,1,1…], то есть в виде цепной дроби с единичным периодом. А число π, которое не может быть корнем многочлена с целочисленными коэффициентами, никакого периода не имеет.
Для любой цепной дроби x (а значит и для любого вещественного числа) найдётся подходящая дробь - цепная дробь, имеющая n элементов, совпадающих с первыми n элементами числа x, причём по мере увеличения n, мы получаем подходящую дробь, значение которой всё более приближено к значению числа x.
У бесконечных цепных дробей возможно наличие периода (бесконечно повторяющегося элементов цепной дроби), такие цепные дроби называются периодическими. В виде периодической цепной дроби может быть представлена только квадратичная иррациональность (то есть такое иррациональное число, которое может являться корнем квадратного уравнения с целыми коэффициентами). Например, золотое сечение (иррациональная математическая константа, являющаяся корнем квадратного уравнения x2-x-1 = 0) представляется в виде цепной дроби [1,1,1,1…], то есть в виде цепной дроби с единичным периодом. А число π, которое не может быть корнем многочлена с целочисленными коэффициентами, никакого периода не имеет.
Для любой цепной дроби x (а значит и для любого вещественного числа) найдётся подходящая дробь - цепная дробь, имеющая n элементов, совпадающих с первыми n элементами числа x, причём по мере увеличения n, мы получаем подходящую дробь, значение которой всё более приближено к значению числа x.
Зачем нужны цепные дроби?
Цепные дроби оказались крайне полезны в математике. В первую очередь ценность имеет тот факт, что не существует более точного рационального приближения для иррационального числа с меньшим знаменателем, чем подходящая дробь. Кроме рациональных приближений, непрерывные дроби так же используются при решении диофантовых уравнений. Не стоит недооценивать их значение в теории чисел и математическом анализе. Благодаря цепным дробям было доказано множество фактов и теорем, например, благодаря цепным дробям была доказана трансцендентность числа π.
Алгоритм разложения числа в цепную дробь
Простейшим алгоритмом преобразования числа в цепную дробь является алгоритм Евклида:
Последовательность чисел a > b > r1 > r2 > r3... > rn определяется тем, что каждый член этой последовательности, начиная с r1 является остатком от деления предпредыдущего числа на предыдущее. Тогда мы можем записать число a как bq0 + r1 , а дробь a/b как q0 + r1/b, затем мы преобразуем дробь r1/b таким образом, чтобы в её числителе осталась единица, получая выражение: a/b = q0 + 1/b/r1, видно, что в знаменателе, дробь b/r1 так же содержит два соседних члена последовательности, а значит мы можем проделать с ней ту же операцию.
Последовательность чисел a > b > r1 > r2 > r3... > rn определяется тем, что каждый член этой последовательности, начиная с r1 является остатком от деления предпредыдущего числа на предыдущее. Тогда мы можем записать число a как bq0 + r1 , а дробь a/b как q0 + r1/b, затем мы преобразуем дробь r1/b таким образом, чтобы в её числителе осталась единица, получая выражение: a/b = q0 + 1/b/r1, видно, что в знаменателе, дробь b/r1 так же содержит два соседних члена последовательности, а значит мы можем проделать с ней ту же операцию.
История появления и развития понятия <<цепная дробь>>
Мы создали таблицу, отражающую историю появления и развития понятия «цепная дробь» от момента её появления и до наших дней. Посмотреть результаты нашей работы можно по ссылке https://disk.yandex.ru/i/Hqd8A6BPAba0Ww
Так же мы отметили всех учёных, сделавших вклад в развитие понятия «цепная дробь» на карте в Padlet https://padlet.com/shnurkigaussa/padlet-f73o7btsc4wixmh9
Так же мы отметили всех учёных, сделавших вклад в развитие понятия «цепная дробь» на карте в Padlet https://padlet.com/shnurkigaussa/padlet-f73o7btsc4wixmh9
Христиан Гюйгенс
Христиан Гюйгенс - талантливый голландский математик, физики и изобретатель, сделавший огромный вклад в развитие оптики, молекулярной физики, астрономии, геометрии и часового дела. С событиями из жизни выдающегося учёного вы можете познакомиться в нашей таблице по ссылке https://disk.yandex.ru/i/TK9LbIM_NkoRmw
Перечень научных работ Христиана Гюйгенса:
Перечень научных работ Христиана Гюйгенса:

- 1651 - опубликованы «Рассуждения о квадрате гиперболы, эллипса и круга».
- 1655 год - Гюйгенс открыл спутник Сатурна Титан и описал кольца Сатурна. Также опубликовывает «Новые открытия в величине круга».
- 1657 год - приложение «О расчётах в азартной игре» к книге его учителя ван Схоотена «Математические этюды». Это было первое изложение зарождающейся теории вероятностей. Гюйгенс заложил её основы, ввёл фундаментальное понятие математического ожидания.
- 1657 год - Гюйгенс издал описание устройства изобретённых им часов с маятником.
- 1659 год - Гюйгенс описал всю систему Сатурна в изданном им сочинении.
- 1659 год - изобретение Волшебного фонаря.
- В конце 1660 годов изобрёл «окуляр Гюйгенса»
- 1673 год - Гюйгенс опубликовал классический труд по механике «Маятниковые часы».
- В 1675 году Христиан Гюйгенс запатентовал карманные часы.
- В 1678 году Христиан выпустил «Трактат о свете».
- В 1678 году Гюйгенс открыл поляризацию света и ввёл «принцип Гюйгенса» - основной постулат волной теории.
- 1682 год - создание Механического планетария. Теорию цепных дробей он применил при проектировании зубчатых колес, что обеспечило высокую точность во взаимном движении моделей планет.
- 1698 год - Последняя книга «ΚΟΣΜΟΘΕΩΡΟΣ sive de terris coelestibus earumque ornatu conjecturae» (на латинском языке; опубликована посмертно в Гааге) — философско-астрономическое размышление о Вселенной.
- 1698 год - Гюйгенс получил для Сириуса расстояние в 28000 астрономических единиц, что примерно в 20 раз меньше истинного (опубликовано посмертно)
Советские и русские учёные, занимавшиеся вопросом цепных дробей
Пафнутий Львович Чебышёв 1821-1894 гг.
С помощью непрерывных дробей исследовал диофантовы приближения и разработал общую теорию разложения произвольной функции в ряд по ортогональным многочленам.
С помощью непрерывных дробей исследовал диофантовы приближения и разработал общую теорию разложения произвольной функции в ряд по ортогональным многочленам.



Леонард Эйлер 1707 - 1783 гг.
Систематизировал знания о цепных дробях, изловив полную теорию.
Систематизировал знания о цепных дробях, изловив полную теорию.
Андрей Андреевич Марков 1856-1922 гг.
Посвящает множество своих работ цепным дробям, используя их для решения многих математических проблем.
Посвящает множество своих работ цепным дробям, используя их для решения многих математических проблем.
Николай Фёдоровоич Дроздов 1862-1953 гг.
Применил цепные дроби к интерполированию и разложению функций в ряды.
Применил цепные дроби к интерполированию и разложению функций в ряды.
